One of the beautiful things about mathematics is the variety of ways to express concepts.
In this lesson, we are going to use the structure of a rational expression
to rewrite it in different forms.

When we worked with polynomials, we worked with the Division Algorithm,
which expressed the division of two polynomials as
a quotient plus a remainder divided by the divisor.

By definition, rational expressions are in essence the "division" of two polynomials.

We are going to look at simple rational expressions to see if we can rewrite them
so to apply the concept of the Division Algorithm by simple modifications to the expression.

You can think of this process as "decomposing" a simple rational expression into an
entity that you called a "mixed number" when working with fractions in elementary school.

The rational expression will be transformed into the form stated by the Division Algorithm:

Under long division, we saw results such as

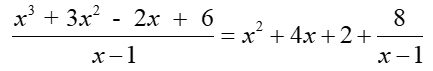
where a rational expression = a quotient + a remainder.

dash

bullet Our task, in the following problems,
will be to convert simple rational expressions into the form of a quotient plus a remainder, i.e, . . .
where a and b are integers.

 

1. Convert:


The trick is to algebraically separate the denominator out of the numerator and see what is left. It is reverse (or expanded) thinking on how to express the numerator.

 

2. Convert:


Be sure the adjusted numerator remains equivalent to the original numerator.

 

3. Convert:


As long as the denominator can be pulled from the numerator, we are up and running.

 

4. Convert:


This is a little more tricky. Plan ahead, and set up the numerator so that the denominator can be pulled out. 3x + 12 = 3(x + 4)

 

5. Convert:


Grouping the appearance of the denominator in the numerator will help avoid careless mistakes.


As you progress in your study of mathematics, you will see this idea, of expressing a rational expression as the addition of components (including fractions), to be developed further. For example, a process called "Partial Fraction Decomposition" is the expression of a rational expression to be the sum of a polynomial (possibly zero) and one or several fractions with a simpler denominator.



divider


NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".