|
Terminalogy Clarification:
 |
The terms "root" and "zero" are encountered when working with equations and functions. |
In mathematics, the terms "root" and "zero" are often used interchangeably.
There is, however, a subtle distinction between these terms.
"Root" is typically used in reference to equations.
"Zero" is typically used in reference to functions (graphs). |
|

"Math" behind solving a quadratic equation:
|
A quadratic equation is a polynomial equation of degree two,
which can be written in the form ax2 + bx + c = 0, where x is a variable and a, b and c are constants with a ≠ 0. |
|
Consider: If a = 0, there would be no x2 term and the equation would be "linear", not "quadratic".
If you know that a quadratic equation (degree 2) has exactly 2 roots, then you
already know (and have used) what is called the "Fundamental Theorem of Algebra".
While there are various statements of this theorem,
the interpretation that we are interested in for this course is the following:
|
The Fundamental Theorem of Algebra: If P(x) is a polynomial of degree n ≥ 1, then P(x) = 0 has exactly n roots, including multiple and complex roots. |
|
In plain English, this theorem says that the degree of a polynomial equation tells
you how many roots the equation will have.
A linear equation (degree 1) will have one root.
 A quadratic equation (degree 2) will have two roots. A quadratic equation (degree 2) will have two roots.
A cubic equation (degree 3) will have three roots.
An nth degree polynomial equation will have n roots.
 Read carefully to fully understand what this theorem is saying. Read carefully to fully understand what this theorem is saying.
• The theorem mentions "multiple" roots . . . so, if a polynomial has a "repeated root", each repetition of the root is counted.
• The theorem mentions "complex" roots . . . so, if a polynomial has a complex root, then the conjugate is also counted since complex roots come in "conjugate pairs".
According to the Fundamental Theorem of Algebra,
a quadratic equation set = 0 has exactly two roots. |
For quadratic equations, the two roots can appear as any one of three forms:
• 2 Real distinct roots
• one repeated Real root
• one Complex conjugate pair
Quadratic Function Graphs illustrate these roots:
The quadratic function graph
may show
2 distinct
real roots
where the graph will
.
cross
the x-axis in
two locations. These
graphs
may open
upward
or downward.
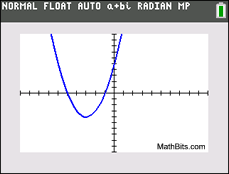 This graph has 2 real zeros.
This graph has 2 real zeros. |
It may appear that the quadratic
function has only one real root.
But,
it
actually has
one repeated root.
This graph
is
tangent to the x-axis
in one
location (touching once).
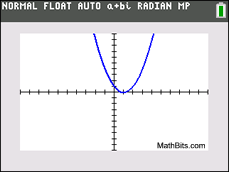 This graph has 1 repeated zero.
This graph has 1 repeated zero. |
The quadratic function may show two
non-real complex roots called
a complex conjugate pair. This
graph will
not cross or touch the
x-axis, but it
has two complex (conjugate) roots.
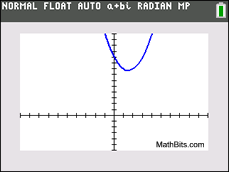 This graph has 2 complex zeros.
This graph has 2 complex zeros. |
Remember, the term "roots" generally refers to equations, while "zeros" refers to functions, but are interchangeable..
In all three situations, there are two solutions to the corresponding quadratic equations,
as stipulated by the Fundamental Theorem of Algebra.

When solving a factorable quadratic equation, each factor can be set equal to zero to find the roots. This process is a fundamental concept known as the Zero Product Property.
|
|
The Zero Product Property: If the product of two or more algebraic expressions equals zero, then at least one of those expressions must equal zero. If a • b = 0, then a = 0, or b = 0, or both a and b equal 0. |
|
This Zero Product Property is an extremely useful property for solving equations that can be factored.
When each factor is
set equal to zero, it is possible to find the solutions (roots) of the equation, and the zeros of the corresponding function.
According to the Zero Product Property,
in
a factored quadratic equation set = 0, you can set each factor = 0. |
Regarding the graph of f (x) = a(x - p)(x - q), we know that the x-intercepts occur at p and q.
The number p and q are called the zeros of the function because the functions's value is zero when x = p and when x = q.
Equation:
x2 + 5x - 24 = 0
(x - 3)(x + 8) = 0
x - 3 = 0 x + 8 = 0
x = 3 x = -8
Function:
f (x) = x2 + 5x - 24
zeros (x-intercepts) at
(3,0) and (-8,0)
|
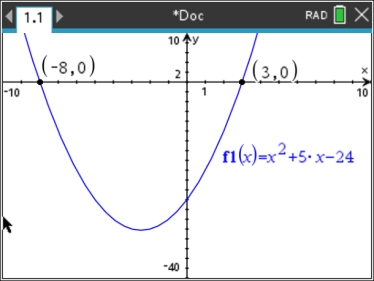 |
The Zero Product Property was applied to the "equation" to arrive at the solutions to the equation. Those equation solutions allowed for finding the locations of the zeros (x-intercepts) of the quadratic function graph.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|




